5. Виды денежных потоков — аннуитеты
Отдельные платежи могут осуществляться строго последовательно, через равные промежутки времени и в равных размерах.
Такая последовательность денежных потоков с равными поступлениями через равные промежутки времени носит название аннуитет.
Примером аннуитета может быть : ежемесячная арендная плата, ежеквартальные перечисления 10% от суммы амортизации в бюджет , начисление амортизации, ежеквартальные выплаты по облигациям.
Если срок действия аннуитета ограничен, аннуитет называется срочным, а если поступления осуществляются неопределенно долго, аннуитет называется бессрочным или вечным.
Денежные поступления могут осуществляться в начале периодов (например, предоплата за аренду помещения -до начала месяца), такой аннуитет называется пренумерандо , а если поступления денег производится в конце периода (оплата за аренду помещения после окончания отчетного периода) — такой аннуитет называется
Представление денежных потоков в виде аннуитета значительно упрощает процессы расчета будущей и приведенной стоимости денег. Т.е. возникает возможность использовать набор упрощенных формул со стандартными значениями отдельных показателей, которые имеются в финансовых таблицах.
Так будущая стоимость аннуитета имеет вид :
Sа = А * Ja
где Sа — общая будущая стоимость аннуитета на конец определенного периода
А — сумма аннуитетного платежа
Ja- множитель наращения аннуитета на конец определенного периода -определяется по специальным финансовым таблицам с учетом процентной ставки и числа периодов.
 , однако запоминать значение и расчет
этого коэффициента нет необходимости,
так как его значение имеется в финансовых
таблицах .
, однако запоминать значение и расчет
этого коэффициента нет необходимости,
так как его значение имеется в финансовых
таблицах .
Пример:
В соответствии с учредительными документами, фирма в конце каждого года направляет в резервный фонд по 30 тыс ден. Ед. Эти деньги вносятся в банк под
13% годовых в течение 5 лет с последующей их капитализацией. Определить будущую стоимость денег через 5 лет
по справочнику Ja= 6.480
проверка : Ja =((1+0.13)5-1)/0.13 = 6,48,
тогда Sa = 6,48*30 000 = 194,4 тыс ден.ед.
Таблица называется «расчет будущей стоимости срочного аннуитета постнумерандо в одну денежную единицу»
(объясните, почему нельзя использовать формулу начисления сложного процента и соответствующие таблицы)
Для расчета настоящей стоимости аннуитета используется формула
Ра=А/Да
где Pa — настоящая стоимость аннуитета
А- сумма аннуитетного платежа
Да — дисконтный множитель аннуитета, определяемый по спец. Таблицам с учетом дисконтной ставки и числа периодов.

I (для описанного выше примера)
Да = 3,517 тогда Ра = 30000/3,517 =8529 ден.ед.
6.Учет инфляции в финансовых расчетах
В финансовых расчетах, при расчетах изменения стоимости денег во времени необходимо учитывать инфляцию., которая вызывает соответствующее снижение покупательской способности денег.
Номинальная сумма денежных средств — сумма денежных средств без учета изменения покупательской способности денег.
Реальная сумма денежных средств — оценка величины денежных средств с учетом изменения покупательской способности денег в связи с процессом инфляции. Учет инфляции в финансовых расчетах производится
-при корректировке будущей стоимости; при формировании уровня ставки процента с учетом инфляции для дисконтирования и определения будущей стоимости.
-при определении уровня доходности по финансовым операциям, учитывающим темпы инфляции.
Темп инфляции -отношение прироста среднего уровня цен в рассматриваемом периоде к базовому уровню цен , выражается в виде десятичной дроби
Ti= ΔЦ/Ц=ΔS/S
Индекс инфляции — единица плюс темп инфляции. Ii =1 + Т i
Если в процессе расчета будущей стоимости проекта (или денежных потоков ) не учитывалась в ставке процента инфляционная составляющая, то
Будущая реальная (наращенная стоимость ) денежных средств с учетом инфляции определяется по формуле: S р = S/ I i
Если при расчете будущей стоимости можно спрогнозировать темп инфляции на определенный период , будущую реальную стоимость денежных средств можно определить следующим образом:
Sp = Р (1+i)n / Ii n = Р (1+ i)n * (1+Ti)-n =

Пример: определить будущую реальную стоимость вложения денежных средств в проект, если объем вложений составил 400 тыс ден.ед. период вложения 3 года используемая номинальная ставка процента 60% годовых, прогнозируемый темп инфляции — 25 %
Sp = 400 ( 1*0.6/1+0.25)3 =838,86 тыс ден.ед.
Какова же реальная ставка процента с учетом темпа инфляции, ?
Jp = J н — Т i
Где J н — номинальная ставка процента с учетом инфляции, сформированная на рынке Jp — реальная ставка процента.
При расчете будущей стоимости денежных средств какого либо проекта при использовании реальной ставки процента возможны 3 варианта изменения будущей стоимости:
Jн = Ti в этом случае увеличение реальной стоимости денежных потоков не произойдет, так как их прирост будет съедаться инфляцией.
Jн > Ti реальная стоимость денежных потоков будет расти несмотря на инфляцию.
Jн < Ti в данной ситуации инвестирование — убыточно, так как доход будет съедать инфляция. Поэтому в 92-ом году даже при номинальной ставке в 300 % годовых банки не хотели давать долгосрочные кредиты, так как высокие темпы инфляции съедали весь доход банка по процентам . Да и сейчас, долгосрочные кредиты банки не дают, так как спрогнозировать темп инфляции очень трудно.
Рассмотрим формирование доходов по финансовым операциям, учитывающим темпы инфляции:
В
этом случае рассчитывается
Пі = Dp * Ti
где Dp — реальный среднерыночный уровень дохода на вложенный капитал (в США — 8 % на вложенный капитал)
Тогда Номинальный доход (D н) по финансовому проекту должен составить :
Dн = Dp + Пі
Зависимость суммы номинального дохода и суммы инфляционной премии от темпа инфляции:
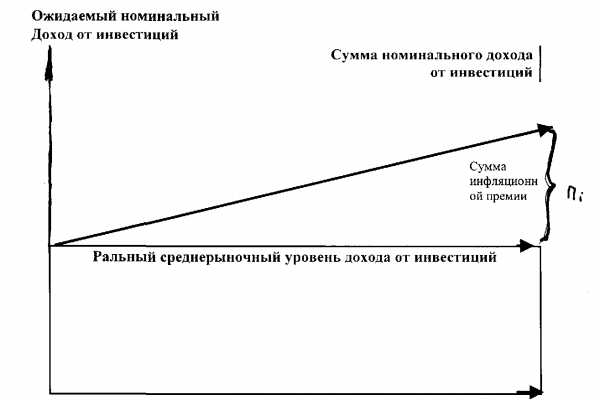 Темп
инфляции
Темп
инфляции
Спрогнозировать темп инфляции очень сложно , то в финансовых расчетах целесообразно учитывают инфляцию более простым способом. Для этого при расчетах будущей и настоящей стоимости денежных потоков в условиях инфляции денежные средства пересчитываются из национальной валюты в «сильную» валюту (в $). Пересчет производят по курсу НБУ на момент проведения расчетов. Затем расчет будущей и приведенной стоимости проекта рассчитывают по процентной ставке процента в соответствующей стране ( при расчете в $ США эта ставка составляет 8-12%)
studfiles.net
Аннуитеты. Понятие и разновидности
Денежный поток с равными интервалами и равными поступлениями денежных средств называется финансовой рентой, или аннуитетом. Различают срочные и бессрочные аннуитеты. По моменту поступления денежных средств в выбранном интервале времени срочные и бессрочные аннуитеты могут быть как потоками пренумерандо, так и потоками постнумерандо. При этом каждый из срочных аннуитетов может рассчитываться как по схеме наращения, так и по схеме дисконтирования.
Классификацию аннуитетов наглядно иллюстрирует рисунок.
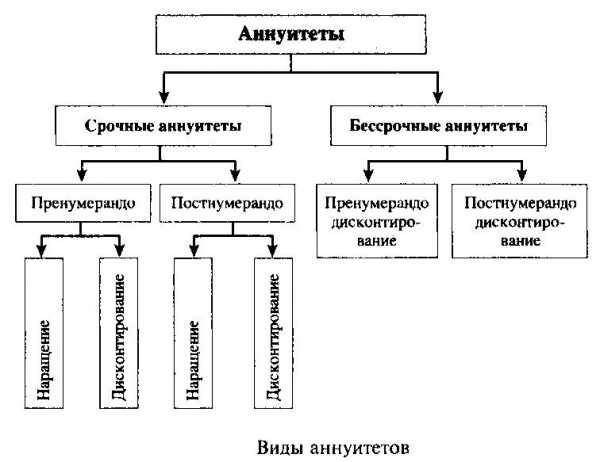
Под срочным аннуитетом понимается денежный поток с поступлениями в течение ограниченного времени (срочный денежный поток) с равными по величине поступлениями денежных средств через равные промежутки времени. По моменту поступления денежных средств различают срочные аннуитеты пренумерандо и постнумерандо.
Срочный аннуитет постнумерандо можно рассчитать как по схеме наращения, так и по схеме дисконтирования.
Формула оценки срочного аннуитета постнумерандо по схеме наращения имеет следующий вид:
FVpst = PV (1 + r)n-1 + PV (1 + r)n—2 + … + PV (1 + r) + PV
Срочный аннуитет пренумерандо можно рассчитать как по схеме наращения, так и по схеме дисконтирования.
Формула оценки срочного аннуитета пренумерандо по схеме наращения имеет следующий вид:
FVpre=FVpst(l+ r) = PV [(1 +r)n— 1] (1 + r)/r.
Формула оценки срочного аннуитета пренумерандо по схеме дисконтирования имеет следующий вид:
PVpre = PVpst(l + r) = FV [1 — (1+r)-n ] (1 + r) / r.
Под бессрочным аннуитетом (вечная рента) понимается денежный поток с равными по величине поступлениями денежных средств в течение длительного срока через равные интервалы времени. Примером бессрочного аннуитета являются консоли (консолидированная рента) — долгосрочные государственные облигации со сроком обращения, превышающим 30 лет.
В случае бессрочного аннуитета поток равных платежей через равные интервалы в течение длительного периода времени рассматривается как бесконечный. При этом подразумевается, что в рамках выбранного интервала осуществляется только один платеж. В этой связи бессрочный аннуитет математически можно представить как бесконечность (n -> ∞) или как бесконечно убывающую геометрическую прогрессию.
Бессрочный аннуитет (как разновидность денежного потока) можно классифицировать по моменту поступлений в выбранном интервале времени на потоки пренумерандо и постнумерандо. Однако, в отличие от других денежных потоков, которые можно рассчитывать как по схеме наращения, так и дисконтирования, оценка бессрочного аннуитета способом наращения не имеет смысла, так как поток стремится к бесконечности и нельзя определить п. Поэтому единственным способом остается обратный способ (способ дисконтирования).
При этом сначала рассчитывается приведенная стоимость бессрочного аннуитета постнумерандо, а затем с его помощью приведенная стоимость бессрочного аннуитета пренумерандо. Классификация способов оценки бессрочных аннуитетов приведена в таблице.
Способы оценки бессрочных аннуитетов
|
По моменту поступления денежных средств в выбранном временном интервале |
Оценка бессрочного аннуитета |
|
|
по схеме наращения |
по схеме дисконтирования |
|
|
1) потоки с поступлениями в начале выбранного интервала времени — пренумерандо; |
Не имеет решения |
Бессрочный аннуитет пренумерандо |
|
2) потоки с поступлениями в конце выбранного интервала времени — постнумерандо. |
Не имеет решения |
Бессрочный аннуитет постнумерандо |
Формула оценки бессрочного аннуитета постнумерандо по схеме дисконтирования имеет следующий вид:
PVpst=A/r,
где А — одно денежное поступление за выбранный временной интервал.
Данная формула показывает, что приведенную стоимость можно рассчитать даже для денежного потока с неограниченным количеством платежей. Так, при сроке аннуитета, превышающем 50 лет, и процентной ставке, равной 10%, разница между значениями коэффициентов дисконтирования незначительная. Чем выше значение процентной ставки, тем меньше срок, при превышении которого разница между значениями коэффициента дисконтирования становится несущественной.
Формула оценки бессрочного аннуитета пренумерандо по схеме дисконтирования имеет следующий вид:
PVpre = PVprs+ A
где PVpre — поток пренумерандо;
PVpre — поток постнумерандо;
А — величина первого платежа.
Как следует из данной формулы, приведенная стоимость бессрочного аннуитета пренумерандо превышает приведенную стоимость бессрочного аннуитета постнумерандо на величину первого платежа.
finance-place.ru
CFA — Как рассчитывать будущую стоимость (FV) последовательности денежных потоков (аннуитета)? | программа CFA
При оценке денежных потоков, последовательно осуществляемых в течение многих периодов времени, обычно используются следующие термины:
- Аннуитет (англ. ‘annuity’) — это ограниченная последовательность (серия) денежных потоков.
- Обычный или простой аннуитет или аннуитет постнумерандо (англ. ‘ordinary annuity’) — это серия денежных потоков, в которой денежные потоки происходят через 1 период, т.е. в начале следующего периода или в конце текущего периода (например, 1-й поток индексируется как t = 1).
- Авансовый аннуитет или аннуитет пренумерандо (англ. ‘annuity due’) — это серия денежных потоков, в которой денежные потоки происходят немедленно, т.е. в начале текущего периода (1-й поток индексируется как t = 0).
См. примеры расчета авансового аннуитета. - Бессрочный аннуитет или перпетуитет или вечная рента (англ. ‘perpetuity’ или ‘perpetual annuity’) — это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. t = 1).
См. пример расчета перпетуитета.
Как вычислять обычный аннуитет, то есть FV равных денежных потоков?
Рассмотрим обычный аннуитет с начислением 5% годовых.
Предположим, что у нас есть 5 отдельных депозитов по $1 000, поступающих с равными интервалами, каждый из которых составляет 1 год, причем 1-й платеж происходит при t = 1.
Наша цель — найти будущую стоимость (FV) этого обычного аннуитета после внесения последнего депозита при t = 5. Поскольку все 5 депозитов вносятся с периодичностью в 1 год, последний платеж осуществляется через 5 лет.
Будущая стоимость (FV) пятилетнего обычного аннуитета.
Как показывает временная линия на рисунке выше, мы находим будущую стоимость каждого депозита на сумму $1 000 к моменту времени t = 5, используя для каждого депозита формулу FV (2):
FVN = PV * (1 + r)N.
Стрелки на рисунке выше соответствуют дате каждого депозита от даты 1-го платежа до t = 5 и указывают на расчет будущей стоимости FV для соответствующего депозита.
Например, по 1-му депозиту в размере $1 000 (при t = 1) будут начисляться проценты в течение 4-х последующих периодов.
Используя формулу FV, мы вычисляем будущую стоимость 1-го депозита при t = 5, которая составляет:
$1 000 * (1,05)4 = $1 215,51.
Для всех других платежей мы вычисляем FV аналогичным образом.
Обратите внимание, что мы находим будущую стоимость при t = 5, поэтому последний (5-й) платеж не важен и не отображается на временной линии.
Теперь, имея все значения FV при t = 5, мы можем их суммировать, чтобы получить будущую стоимость аннуитета, т.е. всей последовательности равных денежных потоков. Эта сумма составляет $5 525,63.
Теперь рассмотрим общую формулу аннуитета, в которой:
- A — сумма аннуитета,
- N — количество периодов и
- r — процентная ставка за период.
Мы можем рассчитать будущую стоимость как
FVN = A * [(1 + r)N-1 + (1 + r)N-2 + (1 + r)N-3 + … + (1 + r)1 + (1 + r)0],
что можно упростить до следующей формулы:
$$\mathbf { FV_N = A \left[ {(1+r)^N — 1} \over r \right] }$$
FVN = A * [((1 + r)N -1) / r] (формула 7)
Выражение в квадратных скобках — это фактор будущей стоимости аннуитета (англ. ‘future value annuity factor’).
Этот коэффициент означает будущую стоимость обычного аннуитета на одну денежную единицу (т.е. на $1 в нашем примере).
Умножение фактора будущей стоимости аннуитета на сумму аннуитета дает будущую стоимость обычного аннуитета.
Для обычного аннуитета, изображенного на рисунке выше, фактор будущей стоимости аннуитета из формулы 7 можно рассчитать как:
[((1.05)5 — 1) / 0.05] = 5.525631.
Если сумма аннуитета A = $1 000, то будущая стоимость аннуитета составляет $1,000 * (5.525631) = $5,525.63, что соответствует вычислению, сделанному ранее.
Следующий пример иллюстрирует, как можно рассчитать будущую стоимость обычного аннуитета, используя формулу 7.
Пример расчета будущей стоимости простого аннуитета.
Предположим, что пенсионный план вашей компании с установленными взносами позволяет вам инвестировать до €20 000 в год. Вы планируете инвестировать €20 000 в год в индексный инвестиционный фонд в течение следующих 30 лет.
Исторически сложилось так, что этот фонд в среднем приносил своим инвесторам 9% в год.
Исходя из того, что вы будете зарабатывать 9% в год, сколько пенсионных средств будет на вашем счете после внесения последнего платежа?
Решение:
Используйте формулу 7, чтобы найти будущую стоимость аннуитета:
A = €20,000
r = 9% = 0.09
N = 30
Фактор FV аннуитета = [(1 + r)N — 1] / r
= [(1.09)30 — 1] / 0.09 = 136.307539.
FVN = €20,000 * (136.307539) = €2,726,150.77.
Предполагая, что фонд будет зарабатывать в среднем 9% в год, вы получите €2,726,150.77 к моменту выхода на пенсию.
Как вычислять аннуитет при неравных денежных потоках?
Довольно часто последовательность денежных потоков аннуитета неравномерна. То есть, потоки денежных средств не являются одинаковыми платежами, осуществляемыми через равные периоды времени.
Это исключает использование в расчете фактора будущей стоимости аннуитета.
Например, у инвестора может быть план сбережений, который предполагает неравные денежные выплаты в зависимости от месяца года или более низкие сбережения во время запланированного отпуска.
В этом случае будущую стоимость серии неравных денежных потоков можно вычислить, рассчитав и суммировав FV каждого отдельного денежного потока.
Пример расчета аннуитета при неравномерных денежных потоках.
Предположим, что у вас есть 5 денежных потоков, которые описаны в таблице ниже. Платежи пронумерованы относительно текущей даты (t = 0).
|
Год |
Денежный
|
Будущая стоимость
|
|
|---|---|---|---|
|
t = 1 |
1,000 |
$1,000 (1.05)4 = |
$1,215.51 |
|
t = 2 |
2,000 |
$2,000(1.05)3 = |
$2,315.25 |
|
t = 3 |
4,000 |
$4,000(1.05)2 = |
$4,410.00 |
|
t = 4 |
5,000 |
$5,000(1.05)1 = |
$5,250.00 |
|
t = 5 |
6,000 |
$6,000(1.05)° = |
$6,000.00 |
|
Сумма = |
$19,190.76 |
||
Все платежи, указанные в таблице выше, отличаются по сумме. Поэтому самый прямой подход к расчету будущей стоимости этих инвестиций при t = 5, — это вычисление FV каждого отдельного платежа при t = 5, а затем суммирование найденных значений FV.
Совокупная FV на 5-й год равна $19,190.76, как показано в третьем столбце таблицы.
fin-accounting.ru
1.3.2 Денежные потоки в виде серии равных платежей (аннуитеты)
Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют финансовой рентой или аннуитетом (annuity).
Теоретически, в зависимости от условий формирования, могут быть получены весьма разнообразные виды аннуитетов: с платежами равной либо произвольной величины; с осуществлением выплат в начале, середине или конце периода и др. [13, 16]
В финансовой практике часто встречаются так называемые простые или обыкновенные аннуитеты (ordinary annuity, regular annuity), которые предполагают получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце каждого периода (года, полугодия, квартала, месяца и.т.д.).
Выплаты по облигациям с фиксированной ставкой купона, банковским кредитам, долгосрочной аренде, страховым полисам, формирование различных фондов – все это далеко неполный перечень финансовых операций, денежные потоки которых, представляют собой обыкновенные аннуитеты. Рассмотрим их свойства и основные количественные характеристики.
Согласно определению, простой аннуитет обладает двумя важными свойствами:
1) все его n-элементов равны между собой: CF1 = CF2 …= CFn = CF ;
отрезки времени между выплатой/получением сумм CF одинаковы, т.е. tn — tn-1 = …= t2 — t1.
В отличии от разовых платежей, для количественного анализа аннуитетов нам понадобятся все выделенные ранее характеристики денежных потоков: FV, PV, CF, r и n.
Будущая стоимость простого (обыкновенного) аннуитета
Будущая стоимость простого аннуитета представляет собой сумму всех составляющих его платежей с начисленными процентами на конец срока проведения операции.
Методику определения будущей стоимости аннуитета покажем на следующем примере.
Пример 1.10
Финансовая компания создает фонд для погашения своих облигаций путем ежегодных помещений в банк сумм в 10000 под 10% годовых. Какова будет величина фонда к концу 4-го года?
FV4 = 10000(1+0,10)3+10000(1+0,10)2+10000(1+0,10)1+10000 = 46410.
Для n-периодов:
. (1.10)
Выполнив ряд математических преобразований над (1.10), можно получить более компактную запись:
. (1.11)
Как уже отмечалось ранее, платежи могут осуществляться j-раз в году (ежемесячно, ежеквартально и т.д.). Рассмотрим наиболее распространенный случай, когда число платежей в году совпадает с числом начислений процентов, т.е. j = m. В этом случае общее число платежей за n-лет будет равно mn, процентная ставка – r/m, а величина платежа – CF/m. Тогда, выполнив преобразования над (1.11), получим:
. (1.12)
Пример 1.11
Предположим, что каждый год ежемесячно в банк помещается сумма в 1000. Ставка равна 12% годовых, начисляемых в конце каждого месяца. Какова будет величина вклада к концу 4-го года ?
Общее количество платежей за 4 года равно: 4 12 = 48. Ежемесячная процентная ставка составит: 12 / 12 = 1%. Тогда:
.
Процентная ставка, равная отношению номинальной ставки r к количеству периодов начисления m, называется периодической.
Следует отметить, что периодическая ставка процентов может использоваться в вычислениях только в том случае, если число платежей в году равно числу начислений процентов.
Текущая (современная) стоимость простого аннуитета
Под текущей величиной (стоимостью) денежного потока понимают сумму всех составляющих его платежей, дисконтированных на момент начала операции.
Определение текущей стоимости денежного потока, представляющего собой простой аннуитет, покажем на следующем примере.
Пример 1.12
Предположим, что мы хотим получать доход, равный 1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?
PV = 1000/l,10 + 1000/(l,10)2 + 1000/(l,10)3 + 1000/(l,10)4 = 3169,87.
Общее соотношение для определения текущей величины аннуитета имеет следующий вид:
. (1.13)
Нетрудно заметить, что выражения в квадратных скобках в (1.13) представляет собой множитель, равный современной стоимости аннуитета в 1 денежную единицу. Разделив современную стоимость PV денежного потока любого вида на этот множитель, можно получить величину периодического платежа CF эквивалентного ему аннуитета. Эта математическая зависимость часто используется в финансовом анализе для приведения потоков с неравномерными поступлениями к виду обыкновенного аннуитета.
Для случая, когда выплаты сумм аннуитета и начисления процентов совпадают во времени, т.е. j = m, удобно использовать соотношение вида:
. (1.14)
Исчисление суммы платежа, процентной ставки и числа периодов
Величину периодического платежа CF и числа периодов проведения операции n для обыкновенного аннуитета можно определить как из соотношения (1.9), так и (1.11).
Если известна будущая стоимость FV, при заданных n и r величина платежа может быть найдена из (1.11):
. (1.15)
При этом выражение в квадратных скобках часто называют коэффициентом погашения или накопления (sinking fund factor).
Соответственно если неизвестной величиной является n, она определяется по формуле:
. (1.16) В случае, если известна текущая стоимость аннуитета PV, формулы для определения CF и n примут следующий вид:
. (1.17)
. (1.18) Выражение в квадратных скобках в (1.17) называют коэффициентом восстановления или возмещения капитала (capital recovery factor).
Исчисление процентной ставки для денежных потоков в виде серии платежей представляет определенные сложности. Используемые при этом итерационные методы обеспечивают получение лишь приближенной оценки и не рассматриваются в настоящей работе. Как будет показано в дальнейшем, современные табличные процессоры позволяют без особых затруднений определять этот важнейший параметр любой финансовой операции. Автоматизация исчисления характеристик аннуитетов
Группу функций EXCEL, предназначенную для автоматизации расчетов характеристик аннуитетов, составляют уже хорошо известные вам функции БЗ(), КПЕР(), НОРМА(), ПЗ() (см. табл. 1.1), к которым добавляется функция определения периодического платежа – ППЛАТ().
Функция ППЛАТ(ставка; кпер; нз; [бс]; [тип])
Данная функция применяется в том случае, если необходимо определить величину периодического платежа – CF.
Предположим, что в примере 1.11 требуется определить размер периодического платежа при заданной будущей величине фонда в 46410.
=ППЛАТ(0,1; 4; 0; 46410) (Результат: -10000,00).
Для банка, в котором размещен данный депозит, периодические платежи означают приток средств, а конечная сумма по депозиту – расход:
=ППЛАТ(0,1; 4; 0; -46410) (Результат: 10000,00).
Обратите особое внимание на значение параметра «нз» (PV). Условиями данной операции наличие первоначальной суммы на депозите в момент времени t = 0 не предусмотрено, поэтому значение параметра «нз» равно нулю. Изменим условия примера 1.10 следующим образом.
Пример 1.13
Финансовая компания создает фонд для погашения обязательств путем помещения в банк суммы в 50000, с последующим ежегодным пополнением суммами по 10000. Ставка по депозиту равна 10% годовых. Какова будет величина фонда к концу 4-го года ?
=БЗ(0,1; 4; -10000; -50000) (Результат: 119615,00).
Соответственно изменится и формат функции для определения величины ежегодного платежа:
=ППЛАТ(0,1; 4; -50000; 119615) (Результат: -10000,00).
В случае, если условиями контракта предусмотрено начисление процентов в начале каждого периода, при исчислении любой характеристики финансовой операции необходимо задавать аргумент “тип”, равный 1.
Для предыдущего примера, функции вычисления будущей величины и периодического платежа будут иметь следующий вид:
=БЗ(0,1; 4; -10000; -50000; 1) (Результат: 124256,00).
=ППЛАТ(0,1; 4; -50000; 124256; 1) (Результат: -10000,00).
Отметим, что начисление процентов в начале каждого периода всегда приводит к большему значению будущей величины аннуитета за тот же срок.
При начислении процентов m-раз в году, величины r и n корректируются также, как и в предыдущих примерах.
Попробуйте самостоятельно построить шаблон для определения количественных характеристик денежных потоков, представляющих собой простой аннуитет. Его можно получить путем несложных преобразований предыдущего шаблона, воспользовавшись командами редактирования ППП EXCEL.
На рис. 1.7 приведен один из простейших вариантов подобного шаблона, который может быть взят за основу. Формулы шаблона приведены в табл. 1.3.
Таблица 1.3
Формула шаблона (аннуитеты)
Ячейка | Формула |
В15 | =БЗ(B5/B6;B7*B6;B10;B8;B11) |
В16 | =НОРМА(B7*B6;B10;B8;B9;B11) |
В17 | =B16*B6 |
B18 | =КПЕР(B5/B6;B10;B8;B9;B11) |
В19 | =ПЗ(B5/B6;B7*B6;B10;B9;B11) |
В20 | =ППЛАТ(B5/B6;B7*B6;B8;B9;B11) |
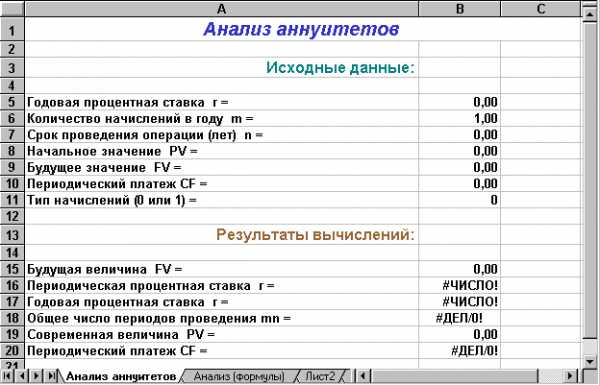
Рис. 1.7. Шаблон для анализа аннуитетов
Сохраните разработанный вами шаблон на магнитном диске под именем ANNUI_AN.XLT.
Проверим работоспособность шаблона на решении следующих типовых задач.
Пример 1.14
Корпорация планирует ежегодно в течении 10 лет делать отчисления по 5000 для создания фонда выкупа своих облигаций. Средства помещаются в банк под 12% годовых. Какая сумма будет накоплена к концу срока операции?
Введем в ячейки колонки В необходимые исходные данные. Полученная в итоге таблица будет иметь следующий вид (рис. 1.8).
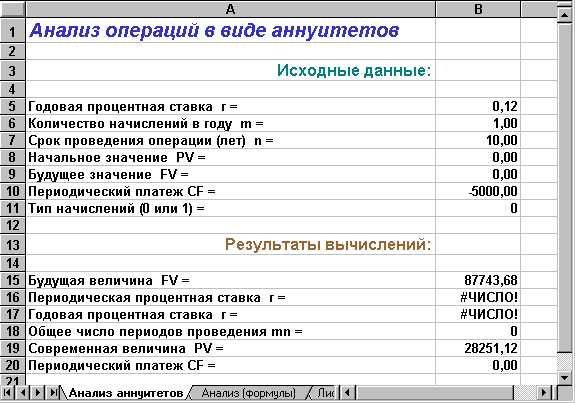
Рис. 1.8. Решение примера 1.14
Величина фонда погашения к концу срока проведения операции составит 87743,68 при начислении процентов в конце каждого периода и 98272,92 при начислении процентов в начале каждого периода (осуществите проверку этого расчета самостоятельно!).
В случае если при решении задач требуется одновременный анализ нескольких альтернатив, скопируйте в соседние колонки необходимое количество раз блок ячеек, содержащий формулы.
studfiles.net
Что такое аннуитет — Всё правильно!
>Услышав слово аннуитет, многие подумают о чём-то очень сложном для понимания. Большинство людей, далёких от экономики, впервые встречаются с этим словом при обращении в банк за кредитом, где им предлагают схему погашения с таким названием.
Термин «аннуитет» происходит от латинского слова annuus — ежегодно. В английском языке есть слово «annual», а во французском — «annuité», которое в переводе означает «годовой», «ежегодный». Современное самое краткое определение аннуитета — это однонаправленные платежи (денежный поток) от кого-либо или к кому-либо, у которых две особенности: периодичность и неизменность суммы. В истории первоначально эти платежи были с периодом, равным одному году, что и стало основанием для названия денежного потока аннуитетом («год» на латинском языке — anno). Сегодня аннуитет — это денежный поток с равными по величине поступлениями и через равные промежутки времени любой продолжительности. Платежи и поступления могут быть ежегодные, ежеквартальные, ежемесячные. Главным остаётся одно: аннуитет — это несколько одинаковых платежей (денежных потоков) через одинаковые промежутки времени. Например, если ваша ежемесячная зарплата постоянна в течение года, то её поступление представляет собой аннуитет с ежемесячным периодом выплаты. Другой пример: при покупке какой-то вещи в рассрочку ваши ежемесячные платежи банку тоже будут аннуитетом.
Для экономистов слово аннуитет имеет три основных значения.
1) В широком смысле – это финансовый инструмент. Например, один из видов срочного государственного займа, по которому ежегодно выплачиваются проценты и погашается часть суммы.
2) Равные друг другу денежные платежи через определённые промежутки времени. Если суммы выплачивают в конце периода, то аннуитет называется обычным, или постнумерандо, а если в начале периода — пренумерандо. Аннуитет бывает немедленный и отложенный, непрерывный и вечный, например, выплаты по облигационным займам с неограниченными сроками. При верном аннуитете платежи подлежат безусловной выплате, а при условном аннуитете платежи ставятся в зависимость от определённого события, например, в личном страховании.
3) Соглашение или контракт со страховой компанией, по которому физическое лицо, начиная с определённого времени (например, с момента выхода на пенсию), приобретает право на регулярное поступление денежных сумм.
Аннуитетом может быть назван не только собственно финансовый инструмент или график выплат, но и сумма периодического платежа.
В качестве примера аннуитета можно рассматривать:
— взносы в пенсионный фонд, если фонд оплаты труда не меняется;
— взносы в счет погашения долгосрочного кредита;
— выплату процентов по ценным бумагам;
— арендные платежи.
В финансовом секторе аннуитет — это разновидность инвестиций, которые приносят вкладчику определённый фиксированный доход через равные промежутки времени (финансовая рента). Он особенно популярен среди современных участников финансового рынка. Это объясняется тем, что аннуитет позволяет легко планировать будущие доходы и расходы. В результате обеспечивается более стабильная и бесперебойная работа любой организации.
Заявка на редактирование текста
comments powered by HyperComments
vsepravilno.com
Аннуитеты в МСФО
В данной статье мы продолжим говорить о дисконтировании денежных потоков и в этот раз речь пойдет об аннуитетных денежных потоках.
Что такое аннуитет?
Аннуитет – это серия одинаковых платежей через одинаковые промежутки времени. Это могут быть ежегодные, ежеквартальные, ежемесячные платежи. Например, фиксированная сумма зарплата, арендных выплат, платежей банку по кредиту и т.д.
Аннуитеты бывают пренумерандо и постнумерандо. Данные термины обозначают момент платежа. Термин пренумерандоозначает платежи в начале каждого периода, постнумерандо — в конце временного периода.
Формула аннуитета
Аннуитетные денежные потоки также можно дисконтировать, то есть определять их текущую стоимость. Например, это необходимо, когда нам нужно выбрать между двумя предлагаемых нам вариантами получения денег.
Дисконтирование аннуитетных платежей
ПРИМЕР 1. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
(Б) 5 раз по 10,000 долларов в конце каждого из следующих 5 лет.
Банковская ставка для получения кредита на данный срок составляет 10%.
На первый взгляд вариант (Б) в сумме лучше (5 х 10,000 = 50,000), чем 40,000 долларов. Но действительно ли это так? Ведь мы знаем, что у денег есть еще и «временная» стоимость. Чтобы сравнить эти два варианта между собой, надо привести их к одному моменту времени (к моменту «сейчас»), поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость.
Для начала давайте вспомним, как выглядит формула дисконтирования:
PV = FV х 1/(1+R)n
где,
Future value (FV) – будущая стоимость Present value (PV) – текущая (дисконтированная/приведенная) стоимость. R – ставка процента (норма доходности, требуемая инвестором), N – число лет от даты в будущем до текущего момента
Коэффициенты дисконтирования, используемые для нашего примера 1/(1+R)n — это 0.9091, 0.8264 и т.д. Только эти вычисления придется повторить 5 раз и сложить. Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая таблица:
10,000 х 0,9091 = 9,091
10,000 х 0,8264 = 8,264
10,000 х 0,7513 = 7,513
10,000 х 0,6830 = 6,830
10,000 х 0,6209 = 6,209
Итого: 37,907
Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В итоге, пять платежей по 10,000 долларов в конце каждого года с учетом дисконтирования стоят 37,907 долларов, что немного меньше, чем 40,000 сегодня. Следовательно, при ставке 10%, 40,000 долларов сегодня будет выгоднее, чем предложенный аннуитет 5 лет по 10,000 долларов.
Формулу дисконтированной стоимости аннуитета можно записать следующим образом:
PV = PMT х [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4 +1/(1+R)5] = 10,000 х (0.9091+0.8264+0.7513+0.6830+0.6209) = 10,000 х 3.7907 = 37,907
где PMT (от английского payment) – это сумма аннуитетного платежа.
Как Вы могли заметить, вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз. Результат сложения коэффициентов дисконтирования за 5 лет называется коэффициентом аннуитета. В данном примере коэффициент аннуитета равен 3,7907.
Таким образом, для нахождения текущей стоимости аннуитетов необходимо разовый платеж умножить на коэффициент аннуитета (10,000*3,7907 = 37,907).
Итак, мы разобрали пример с аннуитетными платежами в конце каждого года (постнумерандо) .
ПРИМЕР 2. Давайте немного изменим условия нашего примера. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
Б) 5 раз по 10,000 долларов в начале каждого из следующих 5 лет.
Это будет так называемый аннуитет пренумерандо.
В данной ситуации, так как первый платеж производится в начале года, то самый важный нюанс, о котором надо помнить, это то что, первый платеж не надо дисконтировать (т.е. приводить к настоящему моменту). Другими словами, для первого платежа используется коэффициент дисконтирования равный единице. Но необходимо дисконтировать остальные 4 платежа, так как они отложены во времени. Для иллюстрации составим следующую таблицу:
10,000 х 1.000 = 10,000
10,000 х 0.9091 = 9,091
10,000 х 0.8264 = 8,264
10,000 х 0.7513 = 7,513
10,000 х 0.6830 = 6,830
Итого: 41,698
Следовательно, предложенный аннуитет 5 лет по 10,000 в начале года будет выгоднее, чем 40,000 сегодня при ставке 10%.
Формула дисконтированной стоимости аннуитета:
PV = PMT + PMT х [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4] = 10,000 + 10,000 х (0.9091+0.8264+0.7513+0.6830) = 10,000 + 10,000 х 3.1698 = 41,698
Обратите внимание, что в данном примере мы определили коэффициент аннуитета для четырех отложенных во времени платежей, а не для пяти, а первый платеж не дисконтировали.
Как видно из данных примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную стоимость аннуитетных денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Все блоги
www.hocktraining.com
CFA — Как рассчитывать текущую стоимость (PV) серии денежных потоков (аннуитета и перпетуитета)? | программа CFA
Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.
Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.
Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.
Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.
Расчет текущей стоимости (PV) серии равных денежных потоков.
Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при t = 1).
Всего простой аннуитет включает N платежей с первым взносом при t = 1 и последним при t = N.
Мы можем выразить текущую (приведенную) стоимость обычного аннуитета как совокупность текущей стоимости каждого отдельного аннуитетного платежа, как указано ниже:
\( \mathbf {PV = {A \over (1 + r)} + {A \over (1 + r) ^ 2} + {A \over (1 + r) ^ 3} + \cdots + {A \over (1 + r)^{N-1}} + {A \over (1 + r)^N}} \) (формула 10)
где:
- A = сумма аннуитета,
- r = процентная ставка за период, соответствующая частоте выплаты аннуитета (например, годовой, ежеквартальный или ежемесячный),
- N = количество аннуитетных платежей.
Поскольку аннуитетный платеж (A) является константой в этом уравнении, его можно вывести за скобки. Таким образом, это выражение можно привести к следующей формуле:
\( \mathbf {PV = A \left [1- {1 \over (1 + r)^N} \over r \right]} \) (формула 11)
Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим текущую стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в формуле 11.
Пример расчета текущей (приведенной) стоимости обычного аннуитета.
Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1 000 каждый год в течение 5 лет с первым платежом через год.
Норма прибыли составляет 12% в год.
Сколько вы должны заплатить за этот актив?
Решение:
Чтобы узнать стоимость финансового актива, используйте формулу (11) текущей стоимости обычного аннуитета, со следующими данными:
A = €1,000
r = 12% = 0.12
N = 5
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \left[ 1-{1\over(1.12)^5} \over 0.12 \right] \end{aligned} } \)
= €1,000 * (3.604776)
= €3,604.78
Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.
Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).
При авансовом аннуитете 1-ый платеж выполняется в текущую дату (t = 0). В общей сложности авансовый аннуитет включает N платежей.
На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.
Авансовый аннуитет в размере $100 за период.
На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:
- единовременная сумма в размере $100 на текущую дату (при t = 0) и
- обычный аннуитет в размере $100 за период в течение 3-х периодов.
При ставке дисконтирования в 12% четыре денежных потока в размере 100$ в этом примере авансового аннуитета будут стоить $340,18.
Существует альтернативный способ расчета текущей стоимости авансового аннуитета.
По сравнению с обычным аннуитетом каждый платеж авансового аннуитета дисконтируется на 1 период раньше.
Поэтому мы можем модифицировать формулу 11, умножив правую часть уравнения на (1 + r):
PV (Авансовый аннуитет) = \( \mathbf {A \left[ 1-(1+r)^{-N} \over r \right] (1+r) } \)
Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.
Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.
Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.
Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:
- немедленную единовременную выплату в размере $2 млн. или
- аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.
Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.
Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.)
Решение:
Чтобы сравнить эти два варианта, необходимо найти текущую стоимость каждого из них в момент времени
t = 0 и выбрать наибольшее значение.
Текущая стоимость первого варианта составляет $2 млн., т.е. первый вариант уже выражен в сегодняшнем эквиваленте.
Второй вариант — аннуитет. Поскольку первый платеж происходит при t = 0, вы можете разделить этот аннуитет на две части:
- немедленную выплату $200 000 от текущей даты (t = 0) и
- обычный аннуитет в размере $200 000 в год в течение 19 лет.
Чтобы рассчитать этот аннуитет, вам нужно найти текущую стоимость обычного аннуитета, используя формулу 11, а затем добавить к нему 200 000 долларов.
A = $200,000
N = 19
r = 7% = 0.07
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= $200\ 000 \left[ 1-{1\over(1.07)^{19}} \over 0.07 \right] \end{aligned} } \)
= $200,000(0.335595)
= $2,067,119.05
19 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.
Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.
Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.
Пример расчета прогнозируемой текущей стоимости обычного аннуитета.
Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при t = 10.
После того, как пособия начнут выплачиваться, эти выплаты продлятся до t = 39, что составляет в общей сложности 30 платежей.
Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионному плану составляет 5% годовых, начисляемых ежегодно?
Решение:
Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при t = 10.
При этом, на момент t = 9 мы имеем обычный аннуитет с 30 платежами. Мы можем вычислить текущую стоимость (PV) этого аннуитета с помощью формулы 11, а затем посмотреть на нее на временной шкале.
A = €1,000,000
r = 5% = 0.05
N = 30
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \ 000 \left[ 1-{1\over(1.05)^{30}} \over 0.05 \right] \end{aligned} } \)
= €1,000,000 * (15.372451)
= €15,372,451.03
Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).
На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от t = 10 до t = 39.
Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени t = 9.
Текущая стоимость (PV) пенсионных пособий по состоянию на t = 9 составляет €15,372,451.03.
Далее задача заключается в том, чтобы найти текущую стоимость на текущую дату (при t = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости (см. CFA — Эквивалентность приведенной и будущей стоимости денежных потоков).
Как показано на временной лини, мы можем рассматривать сумму при t = 9 в качестве будущей стоимости с точки зрения t = 0.
Мы вычислим текущую стоимость (PV) при t = 0 следующим образом:
FVN = €15,372,451.03 (текущая стоимость при t = 9)
N = 9
r = 5% = 0.05
PV = FVN * (1 + r)—N
= €15,372,451.03 * (1.05)-9
= €15,372,451.03 * (0.644609)
= €9,909,219.00
Приведенная стоимость на текущую дату (при t = 0) пенсионного обязательства составляет €9,909,219.00.
Приведенный пример иллюстрирует три процедуры:
Как вычислять текущую стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?
Рассмотрим случай обычного аннуитета, который продолжается бесконечно. Такой обычный аннуитет называется бессрочным аннуитетом или перпетуитетом или вечной рентой (англ. ‘perpetuity’ или ‘perpetual annuity’).
Чтобы получить формулу для текущей стоимости перпетуитета, мы можем модифицировать формулу 10, чтобы учесть бесконечную последовательность денежных потоков:
\( \mathbf {PV = A \sum _{t = 1} ^{\infty} \left[ 1 \over (1 + r)^t \right] } \) (формула 12)
Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:
PV = A / r (формула 13)
Чтобы понять смысл этого преобразования, обратите внимание на формулу (11) текущей стоимости обычного аннуитета.
Поскольку N (количество периодов в аннуитете) переходит на бесконечность, выражение 1 / (1 + r)N приближается к 0, а формула 11 упрощается до формулы 13.
Эта формула потребуется, когда мы будем оценивать дивиденды от акций, поскольку акции не имеют предопределенного срока действия.
Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.
При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.
Формула 13 справедлива только для бессрочного аннуитета с равными платежами. В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.
Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.
Пример расчета текущей стоимости (PV) перпетуитета.
Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.
Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?
Решение:
Чтобы ответить на этот вопрос, мы можем использовать формулу 13 со следующими данными:
A = £100
r = 5% = 0.05
PV = A/r
= £100/0.05
= £2,000
Облигация будет стоить £2 000.
Текущая стоимость на момент времени, отличный от текущей даты (t = 0).
На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от t = 0.
Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим PV1 = $ 100 / 0,05 = $2 000 при 5%-й ставке. Кроме того, мы можем рассчитать PV на текущую дату как PV0 = $2,000 / 1.05 = $ 1,904.76.
Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.
По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.
При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года (t = 3) и $29,99 на текущую дату (t = 0).
Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.
Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.
Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при t = 5.
Какова будет его текущая стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?
Решение:
Во-первых, мы находим текущую стоимость перпетуитета при t = 4, а затем дисконтируем эту сумму к текущей дате t = 0. (Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс t = 4 для нашего расчета текущей стоимости).
1. Находим текущую стоимость перпетуитета при t = 4:
A = £100
r = 5% = 0.05
PV = A/r
= £100/0.05
= £2,000
2. Находим текущую стоимость будущего значения при
t = 4.
С точки зрения сегодняшней даты t = 0 текущую стоимость в £2,000 можно считать будущей стоимостью.
Теперь нам нужно найти текущую стоимость £2,000 при
t = 0:
FVN = £2,000 (текущая стоимость при t = 4)
r = 5% = 0.05
N = 4
PV = FVN * (1 + r)—N
= £2,000 * (1.05)-4
= £2,000 * (0.822702)
= £1,645.40
Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.
Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.
В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при t = 5; после этого платежи продолжаются бесконечно.
Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к t = 5.
Благодаря этому перпетуитет с отсроченной 1-й выплатой (до t = 5) обеспечивает выплаты при t = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.
Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.
Следующий пример иллюстрирует этот результат.
Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.
С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:
- Перпетуитет 1 на £100 в год, начиная с 1-го года (первый платеж при t = 1).
- Перпетуитет 2 на £100 в год, начиная с 5-го года (первый платеж при t = 5).
Решение:
Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при t = 1, 2, 3, 4).
Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:
PV0 (Перпетуитет 1) = £100 / 0.05 = £2,000
PV4 (Перпетуитет 2) = £100 / 0.05 = £2,000
PV0 (Перпетуитет 2) = £2,000 / (1.05)4 = £1,645.40
PV0 (Аннуитет)
= PV0 (Перпетуитет 1) — PV0 (Перпетуитет 2)
= £2,000 — £1,645.40
= £354.60
Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.
Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?
Когда мы имеем неравные денежные потоки, мы должны сначала найти текущую стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.
Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.
В таблице ниже приведена последовательность денежных потоков с
- временными периодами в 1-м столбце,
- денежными потоками во 2-м столбце и
- текущей стоимостью (PV) каждого денежного потока в 3-м столбце.
В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.
|
Период |
Денежный поток ($) |
PV при t=0 |
|
|---|---|---|---|
|
1 |
1,000 |
$1,000(1.05)-1 = |
$952.38 |
|
2 |
2,000 |
$2,000(1.05)-2 = |
$1,814.06 |
|
3 |
4,000 |
$4,000(1.05)-3 = |
$3,455.35 |
|
4 |
5,000 |
$5,000(1.05)-4 = |
$4,113.51 |
|
5 |
6,000 |
$6,000(1.05)-5 = |
$4,701.16 |
|
Сумма = |
$15,036.46 |
||
Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.
Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.
Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду t = 5:
PV = $15,036.46
N = 5
r = 5% = 0.05
FVN = PV * (1 + r)N
= $15,036.46 * (1.05)5
= $15,036.46 * (1.276282)
= $19,190.76
fin-accounting.ru
